정렬이란 지난 글에서 배웠던 이진 탐색이라는 강력한 탐색 방법을 사용하기 위한 준비과정이라고 할 수 있다. 정렬 알고리즘은 종류에 따라서 시간 복잡도의 형태가 다르다. O(n²)인 버블 정렬, 삽입 정렬, 선택 정렬, O(n log n)인 병합 정렬, 퀵 정렬 등이 있고 이 외에도 다양한 정렬 종류가 존재한다.
버블 정렬이란 n번의 라운드로 이루어져 매 라운드마다 원소의 값을 모두 살펴본다. 연달아 있는 두 원소의 값을 비교하여 정렬 순서에 맞지 않을 경우 두 원소의 위치를 바꾼다. 매번 n만큼을 확인하기 때문에 시간 복잡도는 O(n²)으로 비효율적이라고 할 수 있다.
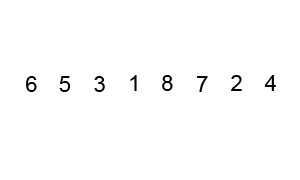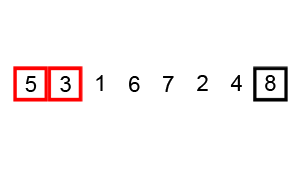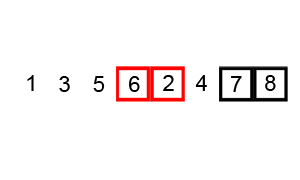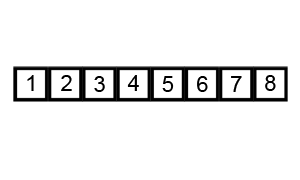
버블 정렬 수도코드
begin BubbleSort(list)
for all elements of list
if list[i] > list[i+1]
swap(list[i], list[i+1])
end if
end for
return list
end BubbleSort선택 정렬이란 처리 되지 않은 데이터를 확인하면서 가장 작은 값을 맨 앞으로 보내는 작업을 반복하는 정렬을 의미한다. 탐색 횟수는 n + (n-1) + (n-2) .... + 2로 이미 정렬된 데이터는 더이상 탐색하지 않기 때문에 버블 정렬보다는 효율적인 방식이다.

선택 정렬 수도코드
list : array of items
n : size of list
for i = 1 to n - 1
min = i
for j = i+1 to n
if list[j] < list[min] then
min = j;
end if
end for
if indexMin != i then
swap list[min] and list[i]
end if
end for
end procedure삽입 정렬은 선택 정렬과 같이 처리 하지 않은 데이터를 확인한다는 점은 같지만 맨 앞으로 옮기는 것이 아닌 적절한 위치에 삽입한다는 점에서 차이가 발생한다. 인접한 두 데이터의 값을 비교하고 자기보다 앞의 데이터 값이 크다면 서로 위치를 바꿔주고 자기보다 작은 데이터 값을 만나면 더이상 이동하지 않는다. 이 방법은 어느정도 정렬 되어있는 배열이라면 빠른 속도를 가질 수 있다는 특징이 있다.

삽입 정렬 수도코드
int holePosition
int valueToInsert
for i = 1 to length(A) inclusive do:
valueToInsert = A[i]
holePosition = i
while holePosition > 0 and A[holePosition-1] > valueToInsert do:
A[holePosition] = A[holePosition-1]
holePosition = holePosition -1
end while
A[holePosition] = valueToInsert
end for
end procedure
퀵 정렬은 피벗을 기준으로 좌우를 나누는 특징을 가지고 있는 정렬 알고리즘으로 피벗보다 큰 데이터와 작은 데이터의 위치를 서로 바꾸는 방식이다. 피벗을 선택하고 이후 왼쪽부터 피벗보다 큰 데이터를 선택하고 오른쪽에서는 피벗보다 작은 데이터를 선택한다. 두 데이터 값의 위치를 서로 바꾼 다음 다시 피벗보다 큰 값과 작은 값을 골라서 서로 위치를 바꿔준다. 반복하다가 서로의 위치가 엇갈리는 경우에는 피벗과 가장 작은 데이터의 위치를 바꿔준다. 이후에 배열의 특징은 피벗을 기준으로 피벗보다 작은값은 왼쪽으로 피벗보다 큰 값은 오른족에 나누어져 있다. 이후 왼쪽 데이터와 오른쪽 데이터 묶음에 대해서도 퀵 정렬을 수행하면 정렬이 완료된다. 퀵 정렬은 이상적인 경우 절반씩 나누어져 O(n log n) 시간 복잡도를 가질 수 있지만 최악의 경우 O(n²)시간 복잡도를 가질 수도 있다. 피벗값과 비교하는 과정에서 n만큼의 원소를 확인해야 할 수 있기 때문이다.

def quicksort(A, lo, hi):
pivot = lo
left = lo +1
right = hi
while (left <= right):
while(left <= hi and A[left]<=A[pivot]):
left += 1
while(right > lo and A[right] >= A[pivot]):
right -= 1
if (left > right):
A[right], A[pivot] = A[pivot] , A[right]
else:
A[left], A[right] = A[right], A[left]
quicksort(A, lo, right -1)
quicksort(A, right + 1, hi)'알고리즘' 카테고리의 다른 글
| 이진 탐색 (0) | 2022.11.16 |
|---|---|
| DFS와 BFS (0) | 2022.11.01 |
| Greedy algorithm (0) | 2022.10.26 |
| Hash_table (0) | 2022.10.21 |


댓글